When it comes to statistics, there’s two schools of thought - frequentism and Bayesianism. In the coming posts we’ll be looking at hypothesis testing and interval estimation and knowing the difference between the two schools is important. In this post I’ll go over what frequentism and Bayesianism are and how they differ.
What is ‘probability’?
The reason for these two schools of thoughts is the difference in their interpretation of probability. For frequentists, probabilities are about frequency of occurence of events. For Bayesians, probabilities are about degree of certainty of events. This fundamental divide in the definition of probability leads to vastly different methods of statistical analysis.
The two schools
The aim of both the frequentists and Bayesians is the same - to estimate some parameters of a population that are unknown.
The assumption of the frequentist approach is that the parameters of a population are fixed but unknown constants. Since these are constants, no statements of probability can be made about them. The frequentist procedures work by drawing a large number of random samples, calculating a statistic using each of these samples, and then finding the probability distribution of the statistic. This is called the sampling distribution. Statements of probability can be made about the statistic.
The assumption of the Bayesian approach is that the parameters of a population are random variables. This allows making probability statements about them. There is a notion of some true value that the parameters can take with certain probability. The Bayesian approach thus allows adding in some prior information. The cornerstone of Bayesian approach is Bayes’ theorem:
Here,
What’s important here is the prior
| Frequentist | Bayesian |
|---|---|
| Parameters are fixed, unknown constants. No statements of probability can be made about them. | Parameters are random variables. Since random variables have an underlying probability distribution, statements of probability can be made about them. |
| Probability is about long run frequencies. | Probability is about specifying the degree of (un)certainty. |
| No statements of probability are made about the data or the hypothesis. | Statements of probability are made about both data and hypothesis. |
| Makes use only of the likelihood. | Makes use of both the prior and the likelihood. |
The procedures
In the frequentist approach, the parameters are an unknown constant and it is the data that changes (by repeated sampling). In the Bayesian approach, the parameters are a random variable and it is the data that stays constant (the data that has been observed). In this section we will contrast the frequentist confidence interval with Bayesian credible interval.
Both confidence intervals and credible intervals are interval estimators. Interval estimators provide a range of values that the true parameters can take.
The frequentist confidence interval
Let’s assume that there’s a true parameter
To be confident that
What this means is that if we were to keep drawing samples and constructing these intervals, 95% of these random intervals will contain the true value of the parameter
Let’s suppose we’re trying to find the average height of men. It is normally distributed with mean
The caveat here is that for simplicity I’ve assumed the critical value to be 2 instead of 1.96 for constructing the interval.
The Bayesian credible interval
A Bayesian credible interval is an interval that has a high posterior probability,
Let’s suppose we’re interested in the proportion of population [1] that gets 8 hours of sleep every night. The parameter
To calculate a Bayesian credible interval, we need to assume a subjective prior. Suppose the prior was scipy as follows:
1 | from scipy import stats |
The 90% credible interval is (0.256, 0.514).
In summary, here are some of the frequentist approaches and their Bayesian counterparts.
| Frequentist | Bayesian |
|---|---|
| Max likelihood estimation (MLE) | Max a posteriori (MAP) |
| Confidence interval | Credible interval |
| Significance test | Bayes factor |
A thing that I have glossed over is handling of nuisance parameters. Bayesian procedures provide a general way of dealing with nuisance parameters. These are the parameters we do not want to make inference about, and we do not want them to interfere with the inference we are making about the main parameter. For example, if we’re trying to infer the mean of a normal distribution, the variance is a nuisance parameter.
The critique
The prior is subjective and can change from person to person. This is the frequentist critique of the Bayesian approach; it introduces subjectivity into the equation. The frequentist approach make use of only the likelihood. On the other hand, the Bayesian criticism of the frequentist approach is that it uses an implicit prior. Bayes theorem can be restated as
The Bayesian criticism of frequentist procedures is that they do not answer the question that was asked but rather skirt around it. Suppose the question posed was “in what range will the true values of the parameter lie?”. The Bayesian credible interval will give one, albeit subjective, interval. The frequentist confidence interval, however, will give many different intervals. In that sense, frequentism isn’t answering the question posed.
Another Bayesian criticism of the frequentist procedures that they rely on the possible samples that could occur but did not instead of relying on the one sample that did occur. Bayesian procedures treat this sample as the fixed data and vary the parameters around it.
The end.
![[Population Scatter Plot]](/2019/03/26/The-Machine-Learning-Notebook-Precision-of-OLS-Estimates/boston_scatter.png)
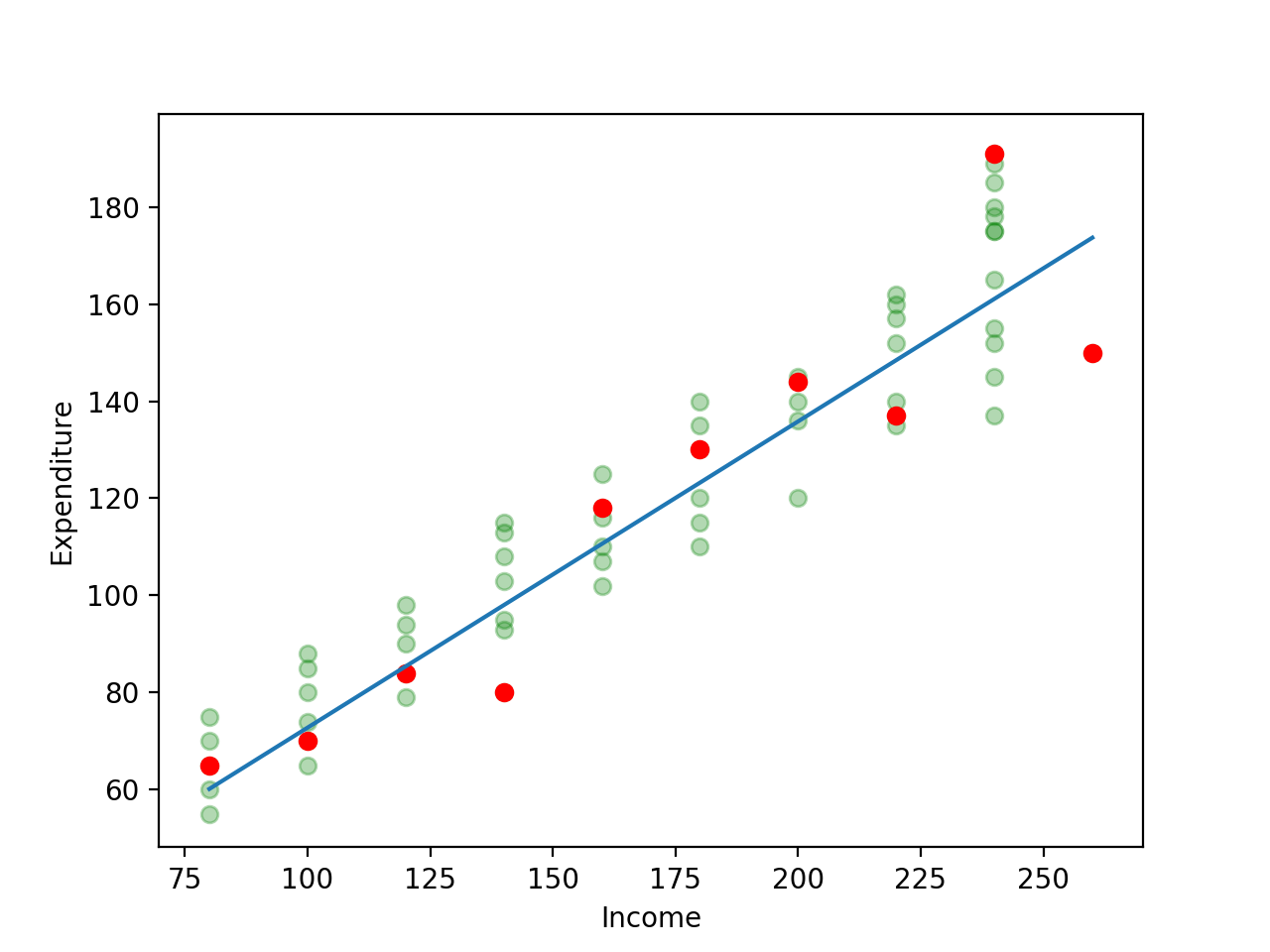
![[Regression Curve]](/2019/03/26/The-Machine-Learning-Notebook-Precision-of-OLS-Estimates/regression_curve.png)