Introduction to Category Theory

We’ve covered a lot of topics in Scalaz but before moving forward, I’d like to cover functors, monoids, monads, etc. These form the basis of functional programming and are predicated in category theory. This post is intended to be an introduction to category theory.

What is Category Theory?

Category theory is a mathematical theory involving the study of categories. A category consists of a group of objects and transformations between them. Think of a category as a simple collection.[1]

Formally, a category consists of the following:

  1. a collection of objects
  2. a collection of arrows (called morphisms)
  3. operations assigning each arrow an object , its domain, and an object , its codomain. We write this as
  4. a composition operator assigning each pair of arrows and , with a composite arrow , satisfying the associative law:
    for any arrows , , and (with , , , and not necessarily distinct),
  5. for each object , an identity arrow satisfying the identity law:
    for any arrow ,
    and

The formal definition above is taken verbatim from Basic Category Theory for Computer Scientists.

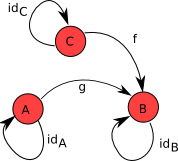
Simple Category

Let’s relate the diagram above[2] to the formal definition that we have. This simple category has three objects , , and . There’s three identity arrows , , and . These identity arrows satisfy the identity law. For example, . Intuitively, if you were “standing” on and you first “walked along” the arrow and then “walked along” the arrow to reach , it’s as good as just “walking along” .

A More Concrete Example

Let’s consider a category whose objects are sets. We’ll translate this into code and hold it to the laws stated above.

  1. is a collection of sets i.e. each object is a set.
  2. an arrow is a morphism from set to set
  3. for each function , we have , and
  4. the composition of a function with is a function from to mapping each element to
  5. for each set , the identity function is a function with domain and codomain as .

Code

Let’s begin by creating our first object of category - a set .

1
2
@ val A = Set("apples", "oranges")
A: Set[String] = Set("apples", "oranges")

Next, let’s define a function which morphs to .

1
2
@ def f(a: Set[String]): Set[String] = a map { _.reverse }
defined function f

Next, let’s morph to by applying the function 

1
2
@ val B = f(A)
B: Set[String] = Set("selppa", "segnaro")

The domain of is the set where as codomain is the set of reversed strings, .

Next, let’s define a function 

1
2
@ def g(b: Set[String]): Set[Int] = b map { _.length }
defined function g

Now let’s compose and 

1
2
@ val C = g(f(A))
C: Set[Int] = Set(6, 7)

And finally, let’s create an identity function

1
2
@ def idA(a: Set[String]): Set[String] = a map identity
defined function idA

Let’s see this in action

1
2
@ idA(A)
res7: Set[String] = Set("apples", "oranges")

This is how we translate a category to code. In the coming posts we’ll cover more category theory.